|
|
| ・鞴(ふいご)の修理は入試問題(2023.1.28) |
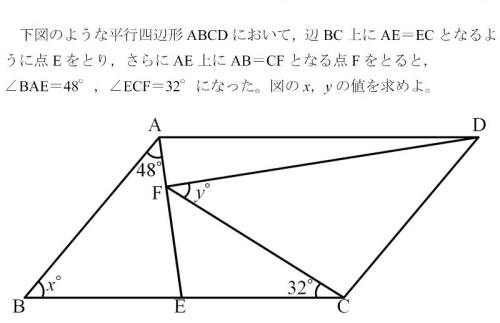 図中xとyの角度を求めよ、某有名私立高校の入試問題です。 ネットの記事に掲載される度、頭の体操代わりについトライして しまいます。ちなみに2枚の絵から違いを探し出すクイズも、 認知症予防になるそうで、見つけると好んで解いています。 *https://hokkaimath.jp/blog-entry-286.htmlより引用 |
||
 鳩時計はhttp://techbase.biz/Repair4/CuckooClock2.htm など、これまでも何台か修理してきました。2018年12月に 修理したhttp://techbase.biz/Repair3/CuckooClock.htm では、鳩(カッコウ)の鳴き声を出すホイッスルに空気を送り 込む鞴(ふいご)の蛇腹が破れ、貼り合わせて修繕しました。 |
||
 今回もまた鳴き声が出ない鳩時計です。鞴と一体に なった高低2個のホイッスル部を取り出します。 |
 鞴の蓋部分が開閉して 蛇腹を伸縮させる構造です。 |
|
 その蛇腹が完全に破れています。 蓋部分は分離・脱落した状態です。 |
 特殊な紙(多分ハトロン紙)で 精巧に折り紙されて作られています。 |
|
 しかし、ここまで完全に破れていると、もはや修繕のしようが ありません。今回は折り紙の構造を解明して、同じ蛇腹を 新しく製作することにします。そのため、蛇腹各部の寸法を 正確に測ることにします。長辺の長さ、54mmほどです。 |
||
 手前短辺の長さは 37mmあります。 |
 蓋の片側が持ち上がり、鞴が開いた 時の開口部の高さを割り出します。 |
|
 破れて分離してしまった双方の長さを 測り、足し合わせることで高さを求めます。 |
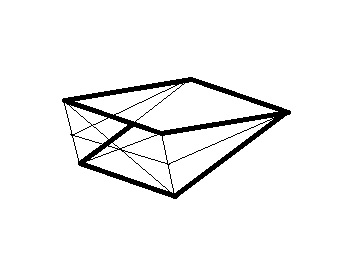 蛇腹の構造をスケッチすると、鞴が 開いた状態でこんな感じになります。 |
|
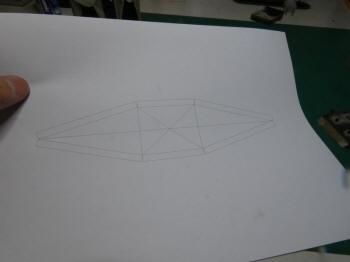 測定した寸法をスケッチに反映させ、 CAD上で正確な展開図を作ります。 |
 作業しやすいように拡大して印刷し 丁寧に切り抜いて型紙にします。 |
|
 1段だけの蛇腹なのでどうってことありません。 折り線に沿って千枚通しで軽くなぞっておきます。 |
 元の蛇腹を参考にしながら、山折り~ 谷折りと楽しく折り紙していきます。 |
|
 ん?、何故か両側面が後方に折れてくれません・・。 説明の余地もなく、この展開図が完全に間違っている ことに気付きます。正面の縦線は垂直ではだめです。 |
||
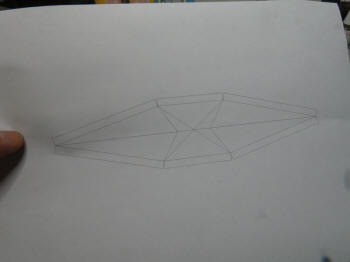 ならば、垂直ではなく内側に倒れ込んで いれば良いのでは。慌てて修正します。 |
 CAD上でデータを修正し、プリンタが 型紙を印刷してくれるので作業は楽です。 |
|
 折り線に傷を入れておくと、簡単かつ 正確に折り曲げることができます。 |
 山折り・谷折りを繰り返し、今度は 側面が後方を向いてくれそうです。 |
|
 1段の蛇腹が綺麗に出来ています。 折り紙もなかなか楽しいものです。 |
 が、蛇腹が閉じて平面になると、なんだ これ・・? 頭にでも付ける飾りかよ。 |
|
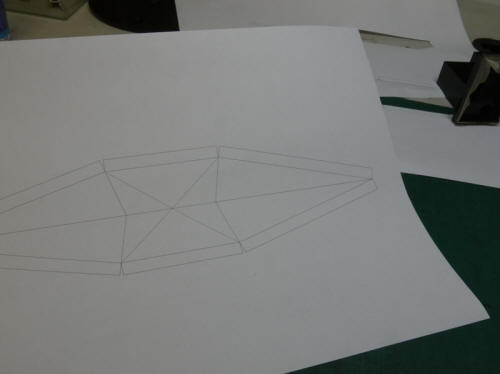 縦線を倒れ込ませ過ぎたようです。気持ち 程度、垂直方向に戻して印刷し直します。 |
||
 折り紙が楽しいのでいいんですけど、この あたりで成功させてしまいたいものです。 |
 左端から右端まで水平に伸びる折り線は 途中で谷折りから山折りに変化します。 |
|
 交差する縦方向と斜め方向の折り線も、山折りと 谷折りに分かれることで蛇腹の形を構成します。 |
 今度はそれっぽく出来たようです。紙製 なので大体で良いように思いますが。 |
|
 折り畳んで平面にした状態で、正面部と側面部が 作る角度を確認します。本来は90度になるはず ですが、スコヤに当ててみると少し開いています。 |
||
 ここまで目検討で調整してきている ので、微妙に合わなくて当然です。 |
 何か法則があるはずです。側面部の斜辺と正面の 縦線が垂直なのでは・・、早速データを修正します。 |
|
 楽しかったはずの折り紙に、疲れて きました。谷折り~山折りを経て、 |
 今度は内側に来てしまいます。斜辺と 垂直にすれば良いわけでもありません。 |
|
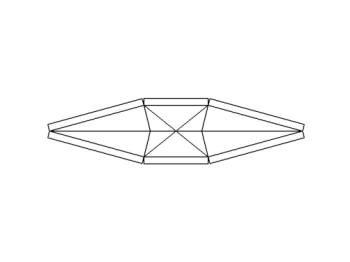 いい加減目検討や当てずっぽうを止めて、 真面目に幾何学的に求めることにします。 |
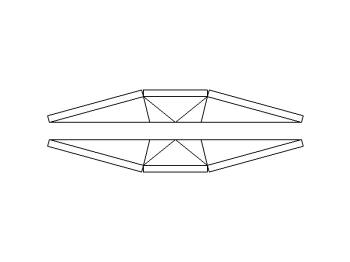 CAD上に描いた展開図です。 まず、上下に2分割します。 |
|
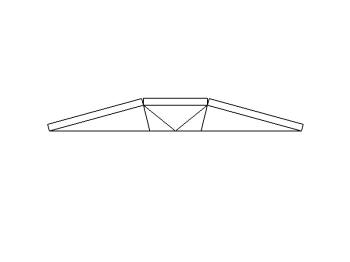 上半分か下半分のどちらかで考えれば 良いので、片方を消しておきます。 |
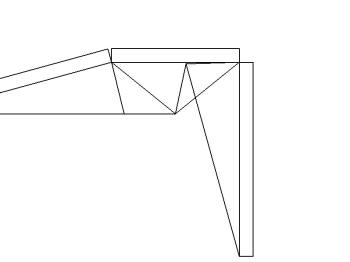 型紙を折って畳んだ状態を描きます。 正面部と側面部が垂直関係になります。 |
|
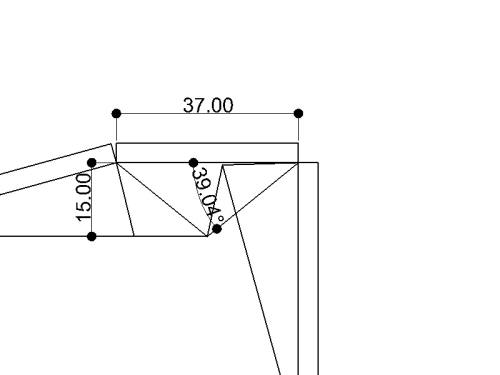 正面の対角線が成す角度を求めます。と言いましても、 CAD上で寸法のメニューから角度を表示させるだけ です。39.04度(≒39度)であることが分かります。 |
||
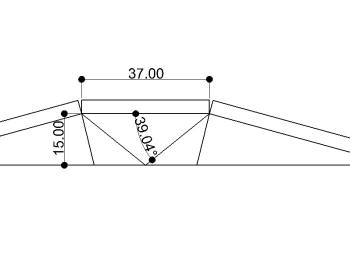 折り畳んでいた側面部を いったん元に戻します。 |
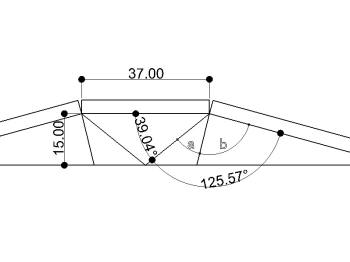 先ほどの対角線と側面部斜辺が成す角度を求めると 125.57度となり、縦線により角aと角bに分割されます。 |
|
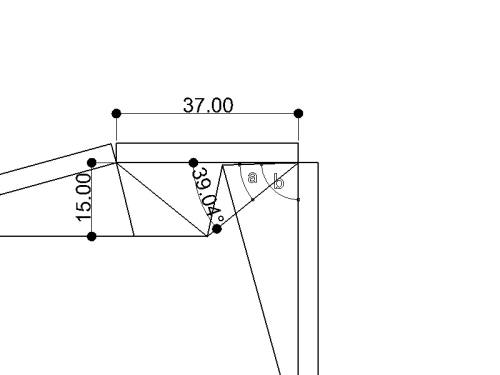 再び折り畳んだ状態にします。合わせて125.57度となる 角aと角bについて、角aは角bの中に含まれた状態です。 ここで知りたいのは角a(または角b)の正確な角度です。 |
||
|
ここで、 a+b=125.57 ・・・① |
||
|
真面目に考えるとこのようになります。正面縦線の 角度は37度、斜辺からは88度でなければならない ことが分かります。まるで冒頭の私立高校入試問題 のようですが、少なくとも私にとっては役に立つ話です。 当てずっぽうで90度だなどと嘘を言ってはいけません。 |
||
 本当に75度で合っているのか、 型紙を作って確かめてみます。 |
 何度も繰り返してきた折り紙、 最後にしたいものです。 |
|
 折り畳んで平面にしてみると、 何となく正確に出来ているような・・ |
 スコヤを当ててみると、 見事に直角です。 |
|
 試作検証を終えて蛇腹製作の本番に入ります。 ハトロン紙の代わりになるものを探します。 |
 これはアクリル板の表面保護に使用されていた薄い シート紙です。片面が樹脂コーティングされています。 |
|
 薄く気密性に富む点でハトロン紙に近いと思います。 紙の固さや強度はやや劣るかも知れません。 |
 実寸のサイズで型を印刷します。 高低の鳴き声用に2枚必要です。 |
|
 スケールを正確に当てて 慎重にカットします。 |
 鞴本体に貼り付けて固定するため、 5mm幅の糊代を付けています。 |
|
 切り抜きを終え、折り線に 沿って軽くけがきます。 |
 山折り~谷折りを進めます。 なかなかシャンとした紙です。 |
|
 蛇腹部分の構成は、無理せず だましだまし折り曲げます。 |
 紙が薄いので蛇腹のみでは 簡単に形が崩れてしまいます。 |
|
 折り線にスケールを当て 糊代部を折り返します。 |
 折り紙の完成です。実寸サイズでの 加工なので細かな作業になります。 |
|
 蛇腹2組の完成です、ここまで長い道のりでした。鞴として ホイッスルに十分な風を送り込むことが出来るでしょうか。 |
||
 鞴に残っている破れた蛇腹を 取り除かなければなりません。 |
 綺麗に剥がし取るために 40℃くらいで湯煎します。 |
|
 念のためひと晩 浸け置きにします。 |
 ハトロン紙はなかなか丈夫で 自然に剥がれてなど来ません。 |
|
 それどころか鞴に接着されていた 糊代部に接着剤が残ったままです。 |
 止むを得ず固着した接着剤を リュータで削り落とします。 |
|
 完成している蛇腹を仮組みして みます。寸法はぴったりのようです。 |
 樹脂部品に紙を貼り付ける 適当な接着剤が分かりません。 |
|
 安直ですが、ゴム系のボンドを使用します。 伸び、乾燥時間など適切とは言えませんが。 |
 ドライバーの先を使って、薄く 伸ばしながら塗り付けます。 |
|
 手前側の短辺と両側面の 長辺に接着剤を塗ります。 |
 紙相手に接着力が強過ぎるので 慎重かつ一発勝負で位置を決めます。 |
|
 手前短辺→両サイド長辺の順で 糊代面を押さえ付け固定します。 |
 何とか形になってきました。 左右の高低とも貼り付けます。 |
|
 上に載る蓋部分を当ててみます。 やはり寸法はぴったりです。 |
 後方の短辺は鞴の回転軸に なるので、ヒンジを当てます。 |
|
 マスキングテープを 適当にカットします。 |
 後方の短辺、鞴の上下を連結 するようにテープを貼り付けます。 |
|
 耐久性に不安はありますが、2重・3重貼りに して蛇腹の動作を重くするわけにも行きません。 |
 上下の位置を合わせた状態で 蛇腹の糊代を周囲に接着します。 |
|
 もう片方も同じように 貼り付け接着します。 |
 左右とも蛇腹の貼り付け、鞴の組み立てを 終えます。全体の納まりを確認します。 |
|
 試しに鞴を軽く開け閉めしてみます。「ポッポー(カッコー?)」の 発声が蘇ります。心持ち、キレというか甲高さが足りないような 気がしますが、古くから親しまれてきた鳩時計の鳴き声です。 |
||
 ホイッスル部をムーブメント本体に 戻し、周辺部品を取り付けます。 |
 ムーブメントから出る鞴を駆動用の アームを取り付けなければなりません。 |
|
 鞴の脇にアームが連結 する突起が出ています。 |
 アームの先を突起の穴に通し、 根元側をムーブメントの軸に掛けます。 |
|
 高低2つの鞴それぞれに アームを取り付けます。 |
 修理作業完了です。鳩(カッコウ)が 元気よく飛び出して軽快に鳴きます。 |
|
 実は、ムーブメント側の鞴駆動軸が固着していたり、鳩の駆動 リンクが変形していたりして、各部に渡り修理を施しています。 時針も折れ曲がり汚れて変色していたので、同色でペイントし 直しています。先にも書きましたが、中学高校入試に出題される 図形問題を解く知識は、私にとってはこのように大いに仕事の 役に立つ有用なものです。しかし、これから入試に挑む小学生や 中学生にしてみると、いったい何を期待し、如何に納得しながら このような学力を身につけるべく努力をすれば良いのでしょう。 |
||
|
||